自动机与程序分析
最早在程序分析中遇到自动机,是在学IFDS的时候(比如这里),里面需要根据call和return指令,做类似括号匹配的操作。
自动机基础
参考 《形式语言与自动机导论%20%20(原书第三版)_11454864.pdf》
下推自动机(Push Down Automata, PDA)
背景知识是,编译原理中,有限状态自动机和正则表达式的知识。另外,也需要一些上下文无关语言的知识。
下推自动机,在有限状态自动机上,额外增加了一个栈,每次转换状态的时候,允许向栈上压入,或弹出元素。
这里介绍一个例子,我们想要匹配偶数长度的,包含a,b两种字符的回文字符串。可以定义一个语法如下:
1 | R -> aRa | bRb | ε |
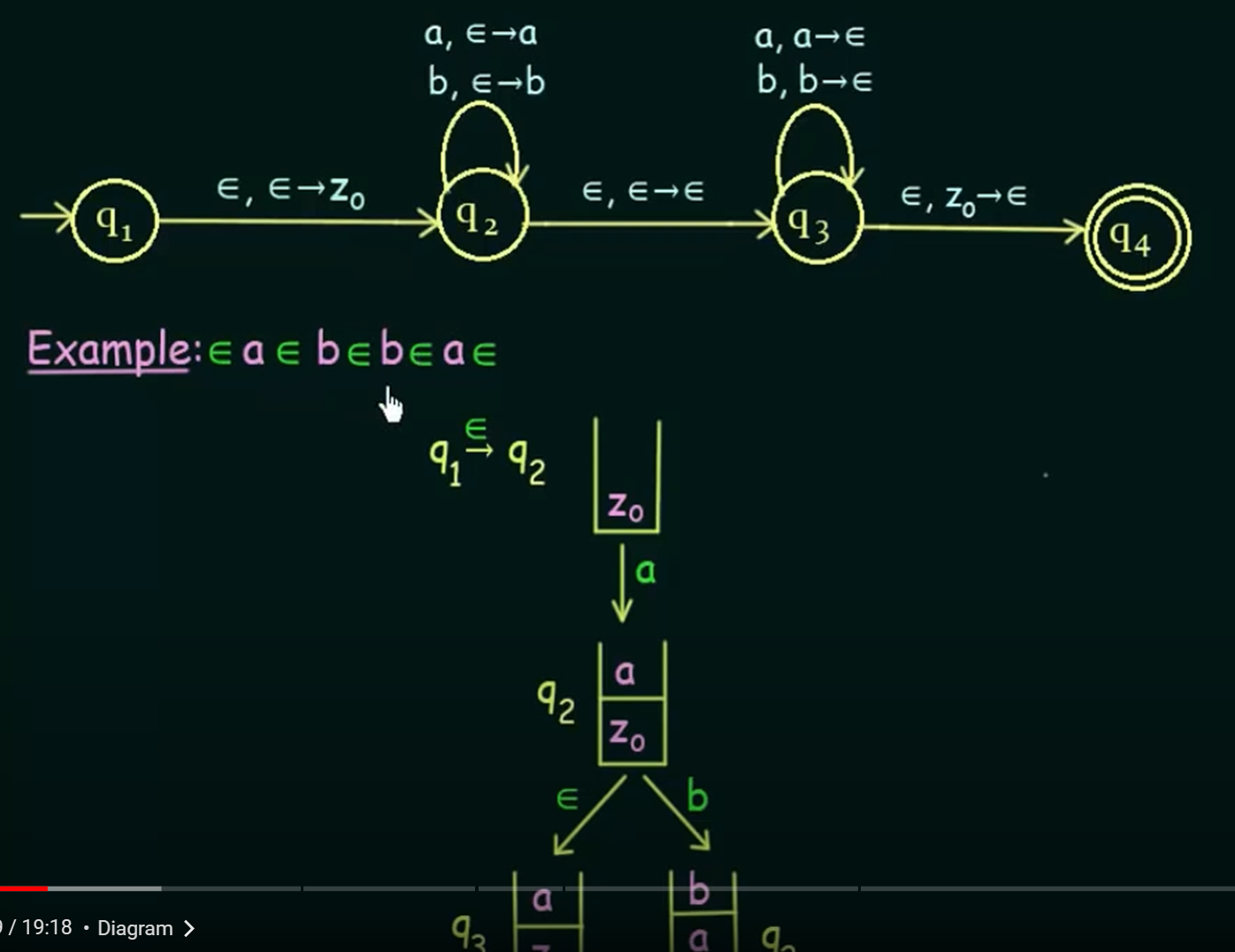
同时,我们可以定义一个下推自动机(来自这个youtube视频)。自动机包含四个状态:
- 初始状态q1:读入ε空字符(不读入字符),同时把开始符号Z0压到栈中,可以转换到状态q2
- q2:读入字符a,或字符b,同时把字符压入栈中,可以转换到状态q2(不变)。或者直接转换到状态q3。
- q3:读入字符a,或字符b,同时弹出相应字符,可以转换到状态q3(字符和栈操作绑定,必须完整执行,否则不能转换)。弹出栈顶Z0符号后可以转换到结束状态q4
- 如果字符串走到了q4状态,且输入结束了,则表示自动机接受了这个输入。
这里是不确定性下推自动机,按规则走时有多条路径。只要有可能走到结束,则说明该字符串被接受。其他情况是有可能走不下去的。
下推自动机和上下文无关语言的一致性:
这里称上下文无关语言为Context Free Grammar, CFG。下推自动机被称为Push Down Automata, PDA。
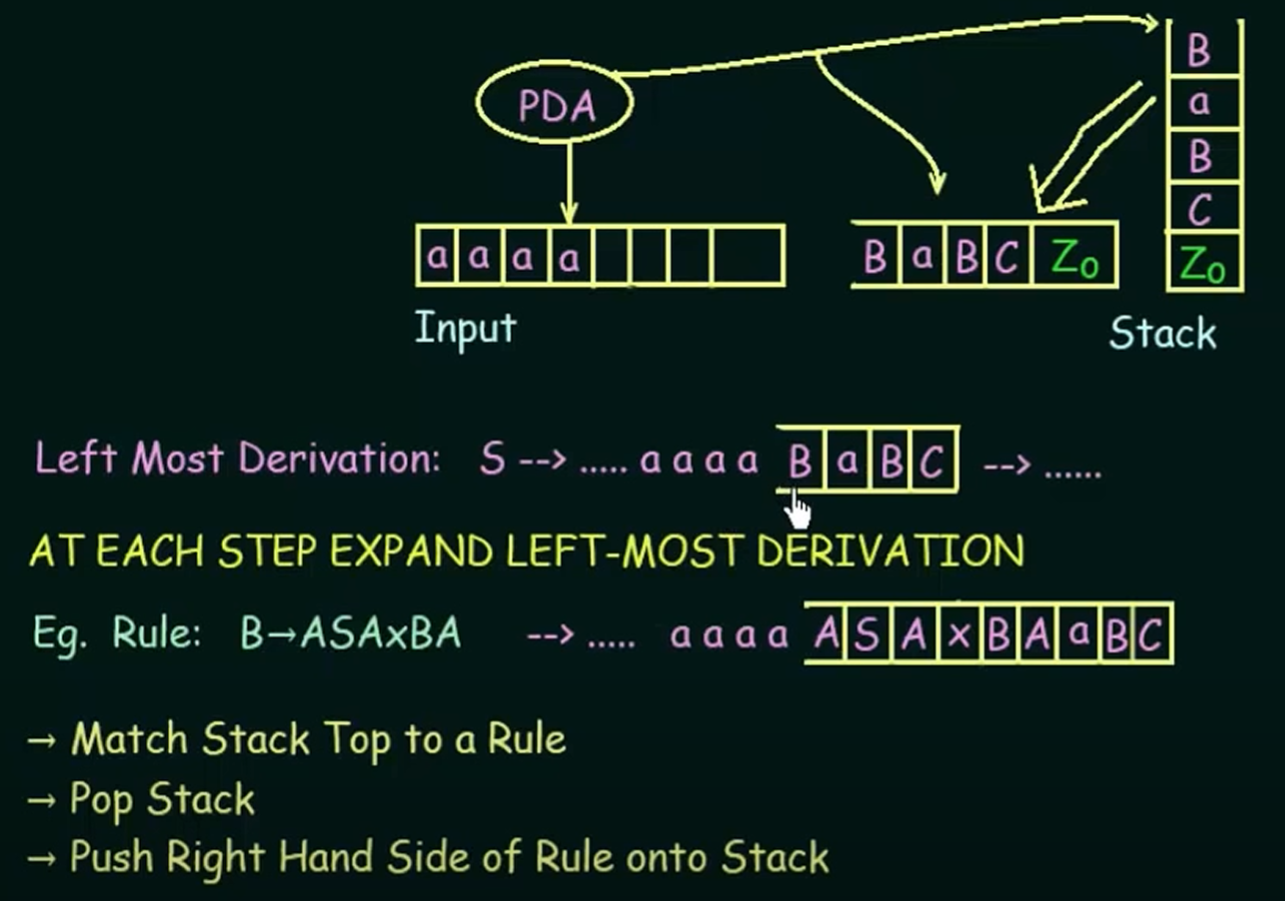
如何把CFG转为PDA? - 在CFG根据规则替换非终结符的时候,我们约定每次仅替换最左侧的终结符。 - 对于每个状态正在推导的CFG,它包含终结符和非终结符的混合序列。我们从最左侧开始扫描,遇到的所有终结符放在PDA的输出上,剩下的放在PDA的栈里。 - 我们每次看栈上最左侧的非终结符,然后看它有哪些规则,比如R -> aRa,我们对应此时有PDA的状态转换规则,即将这个非终结符替换成对应规则应用后的结果,即此时对当前状态有规则,弹出栈上的R,压入aRa,转换到下一个状态。 - 如果栈上是终结符,此时允许读入相同的终结符,弹出栈顶上的这个终结符。
对于CFG,我们有时候不知道用哪个推导规则合适,这个正好对应上不确定性的自动机中,有多种状态转移,不知道转移为哪一种最后能到终态。因此,虽然有这种转换,但是并不代表能够高效解决确定字符串是否属于语言的问题。
什么是 CFL Reachability Problem
阅读《Interconvertibility of Set Constraints and Context-Free Language Reachability》
我们知道普通的有向图的可达问题。但是这种图可达性太简单了。比如,多个函数的控制流图,它首先把每个函数的控制流图放上来,然后对于call指令,增加call指令到被调用函数开头的调用边,以及被调用函数结束时,返回call指令继续执行的边。这样构建出来的图会发现存在一个问题,即没有考虑到返回的时候要根据调用栈返回的情况。返回的时候,由于边就是连着的,直接看可达性的话我可以返回到任意调用点之后继续执行,然而实际情况是只会根据之前call是从哪里过来的,然后返回那边执行。
CFL Reachibility问题,就是结合CFG,给图可达性问题增加一些限制。
首先,我们允许对有向图上每一条边上都标上CFG里的终结符或者非终结符。对于每一条路径,把边上标记的符号连起来就是一个字符串。如果这个字符串属于某个CFG语言,即这个字符串能从CFG的开始符号S,通过CFG语法规则推导得到,则我们称这条路径属于S-Path。
all pair版本的图可达问题,就是求出所有的这样顶点对 v1, v2,使得v1能走到v2。我们定义all pair版本的S-Path问题为,找出所有的顶点对,使得存在一条v1到v2,且属于S-Path的路径。